علوم و تحقیقات
تحقیق و پژوهش، مشاوره مدیریت، پژوهش های سازمانی و دانشجوییعلوم و تحقیقات
تحقیق و پژوهش، مشاوره مدیریت، پژوهش های سازمانی و دانشجوییبحث بسیار کاربردی مشتق
منبع: ویکی پدیا
این مطالب را حتما با دقت تا انتها بخوانید. مطمئن باشید ضرر نمی کنید مشتق تابع
مشتق تابع
اگر 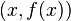 نقطهای از نمودار تابع
نقطهای از نمودار تابع 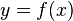 و
و  نقطهٔ دیگری از این نمودار باشد، آنگاه
نقطهٔ دیگری از این نمودار باشد، آنگاه  و شیب خط قاطع عبارت است از:
و شیب خط قاطع عبارت است از:
کسر فوق، خارج قسمت تفاضلی  در
در  نامیده میشود. اگر
نامیده میشود. اگر  ثابت نگه داشته شود و
ثابت نگه داشته شود و 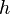 به سمت صفر میل کند، آنگاه خارج قسمت تفاضلی
به سمت صفر میل کند، آنگاه خارج قسمت تفاضلی  در
در  اگر فقط به
اگر فقط به  بستگی داشته باشد به مقداری میل میکند که به آن شیب خط مماس گفته میشود. به عبارت دیگر، حاصل حد زیر در صورت وجود ضریب زاویهٔ خط مماس نمودار تابع
بستگی داشته باشد به مقداری میل میکند که به آن شیب خط مماس گفته میشود. به عبارت دیگر، حاصل حد زیر در صورت وجود ضریب زاویهٔ خط مماس نمودار تابع  در
در  را بدست میدهد:
را بدست میدهد:
تعریف مشتق
برای تابع  که در همسایگی نقطهٔ
که در همسایگی نقطهٔ  تعریف شدهاست، اگر
تعریف شدهاست، اگر 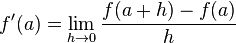 وجود داشته باشد،
وجود داشته باشد،  در
در  مشتقپذیر است. این حدیکتا را با
مشتقپذیر است. این حدیکتا را با  نمایش داده و آن را مشتق تابع
نمایش داده و آن را مشتق تابع  در نقطهٔ
در نقطهٔ  مینامند.
مینامند.
بر طبق این تعریف، مقدار مشتق برابر نرخ تغییرات مقدار تابع است زمانی که تغییرات مربوط به متغیر مستقل به سمت صفر میل میکند.
با تبدیل 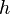 به
به  تعریف دوم مشتق به صورت زیر حاصل میشود:
تعریف دوم مشتق به صورت زیر حاصل میشود:
نمادهای مشتق
لایبنیتس، نیوتون، لاگرانژ، آربوگاست و اویلر هر یک نماد جداگانهای را برای نمایش مشتق بکار میبردند؛ اما در میان پیشگامان اولیهٔ آنالیز ریاضی، لایبنیتس بیش از هر کس دیگری به اهمیت علامات مناسب پی برده بود. او علامات را با حوصلهٔ زیادی آزمایش میکرد و با سایر ریاضیدانان مکاتبات بسیاری داشت و از این طریق معایب و محاسن نمادهای مختلف را برای آنها مطرح میساخت. پیشرفت حساب دیفرانسیل و انتگرال و گسترش ریاضیات نوین تا حدود زیادی بواسطهٔ علامتهای پیشرفتهای است که بسیاری از آنها توسط لایبنیتس ابداع شدهاند.
لایبنیتس در سال ۱۶۷۵ میلادی با استفاده از عملگر تفاضلی  خارج قسمت تفاضلی
خارج قسمت تفاضلی  را به شکل
را به شکل  نوشت و برای مشتق تابع
نوشت و برای مشتق تابع  در
در  نماد
نماد 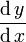 را معرفی کرد که به صورت
را معرفی کرد که به صورت  نیز نوشته میشود. این نماد که نمایش دیفرانسیلی مشتق نامیده میشود، برای نمایش مشتق مراتب بالاتر به شکل
نیز نوشته میشود. این نماد که نمایش دیفرانسیلی مشتق نامیده میشود، برای نمایش مشتق مراتب بالاتر به شکل 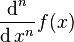 نوشته میشود. با استفاده از این نماد تعریف مشتق به صورت
نوشته میشود. با استفاده از این نماد تعریف مشتق به صورت  در میآید.
در میآید.
نیوتون برای نشان دادن مشتق اول از  و برای مشتق دوم از
و برای مشتق دوم از  استفاده میکرد. نمادهای نقطهدار نیوتون در برخی مسائل فیزیکی مانند سرعت و شتاب بکار میروند.
استفاده میکرد. نمادهای نقطهدار نیوتون در برخی مسائل فیزیکی مانند سرعت و شتاب بکار میروند.
مشتق تابع  را با
را با 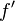 نیز میتوان نشان داد. این نماد بر آن تأکید دارد که
نیز میتوان نشان داد. این نماد بر آن تأکید دارد که 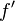 تابع جدیدی است که با مشتقگیری از تابع
تابع جدیدی است که با مشتقگیری از تابع  بدست آمدهاست و مقدارش در
بدست آمدهاست و مقدارش در  با
با  نموده میشود. مختصات
نموده میشود. مختصات  و
و 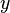 واقع بر نمودار
واقع بر نمودار  با معادلهٔ
با معادلهٔ 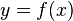 به هم مربوط میشوند، و علامت
به هم مربوط میشوند، و علامت  نیز برای نمایش
نیز برای نمایش  بکار میرود که مقدارش در
بکار میرود که مقدارش در  به صورت
به صورت  نوشته میشود. این نماد در سال ۱۷۷۰ میلادی توسط ژوزف لویی لاگرانژمورد استفاده قرار گرفت و مشتق مراتب بالاتر را به صورت
نوشته میشود. این نماد در سال ۱۷۷۰ میلادی توسط ژوزف لویی لاگرانژمورد استفاده قرار گرفت و مشتق مراتب بالاتر را به صورت 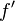 (مشتق اول)،
(مشتق اول)،  (مشتق دوم)،
(مشتق دوم)، 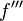 (مشتق سوم)،
(مشتق سوم)،  (مشتق چهارم) ...
(مشتق چهارم) ... 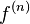 (مشتق
(مشتق 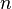 ام) نشان میدهد.
ام) نشان میدهد.
در سال ۱۸۰۰ میلادی نماد دیگری توسط لوییس آربوگاست معرفی شد و توسط لئونارد اویلر مورد استفاده قرار گرفت. این نماد مشتق  را به شکل
را به شکل 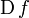 نشان میدهد. علامت
نشان میدهد. علامت  یک عملگر دیفرانسیلی است و این فکر را القا میکند که
یک عملگر دیفرانسیلی است و این فکر را القا میکند که 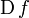 تابع جدیدی است که با مشتقگیری از
تابع جدیدی است که با مشتقگیری از  بدست آمدهاست. مشتق مراتب بالاتر به صورت
بدست آمدهاست. مشتق مراتب بالاتر به صورت 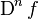 و مقدار آن در
و مقدار آن در  به صورت
به صورت  نوشته میشود.
نوشته میشود.
مشتقهای یک طرفه
مشتق راست: اگر تابع  در فاصلهٔ
در فاصلهٔ 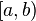 تعریف شده باشد آنگاه حاصل حد زیر، در صورت وجود، مشتق راست تابع در
تعریف شده باشد آنگاه حاصل حد زیر، در صورت وجود، مشتق راست تابع در  میباشد:
میباشد:
مشتق چپ: اگر تابع  در فاصلهٔ
در فاصلهٔ ![(c , a] \!](http://upload.wikimedia.org/math/d/0/0/d008bd5ea6220f5c93a797b99fc34912.png) تعریف شده باشد آنگاه حاصل حد، زیر در صورت وجود، مشتق چپ تابع در
تعریف شده باشد آنگاه حاصل حد، زیر در صورت وجود، مشتق چپ تابع در  میباشد:
میباشد:
مشتقپذیری
تابع  در
در  مشتقپذیر است هرگاه در این نقطه پیوسته باشد و مشتق چپ و راست تابع با هم برابر و مساوی یک عدد حقیقی معین باشد.
مشتقپذیر است هرگاه در این نقطه پیوسته باشد و مشتق چپ و راست تابع با هم برابر و مساوی یک عدد حقیقی معین باشد.
تعبیر هندسی مشتقپذیری: تابع  در
در  مشتقپذیر است هرگاه بتوان در این نقطه یک خط کامل مماس و غیر موازی با محور yها بر منحنی رسم کرد.
مشتقپذیر است هرگاه بتوان در این نقطه یک خط کامل مماس و غیر موازی با محور yها بر منحنی رسم کرد.
اگر تابع  در نقطهٔ
در نقطهٔ  مشتقپذیر باشد، آنگاه در آن نقطه پیوسته نیز هست.
مشتقپذیر باشد، آنگاه در آن نقطه پیوسته نیز هست.
ولی عکس قضیهٔ فوق صحیح نمیباشد یعنی ممکن است تابع پیوسته باشد اما مشتقپذیر نباشد؛ به عبارت دیگر، پیوستگی تابع در  شرط لازم برای مشتقپذیری تابع است، نه شرط کافی. پس اگر تابع
شرط لازم برای مشتقپذیری تابع است، نه شرط کافی. پس اگر تابع  در
در  ناپیوسته باشد، آنگاه در
ناپیوسته باشد، آنگاه در  مشتقپذیر نیست.
مشتقپذیر نیست.
موارد مشتقناپذیری
مواردی که تابع در نقطهٔ مفروض  مشتقپذیر نیست:
مشتقپذیر نیست:
- نقاط ناپیوسته: تابع در نقاط ناپیوسته مشتقناپذیر است و از دید هندسی نمیتوان در این نقاط مماس بر منحنی رسم کرد.
- نقاط زاویهدار: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها دو عدد حقیقی نابرابر، یا یکی عدد و دیگری بینهایت باشد، مشتقپذیر نیست. از دید هندسی، در این نقاط دو نیممماس بر منحنی رسم میشود که با هم زاویه میسازند.
- نقاط عطف قائم: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها بینهایتهای همعلامت باشد مشتقناپذیر است. از دید هندسی، در این نقاط میتوان یک خط کامل مماس به موازات محور yها رسم کرد. نقطهٔ عطف قائم تنها نقطهای است که تابع در آن مشتقپذیر نیست ولی مماس کامل دارد.
- نقاط بازگشت: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها بینهایتهای غیر همعلامت باشد مشتقناپذیر است. از دید هندسی، در این نقاط میتوان یک نیممماس، به موازات محور yها رسم کرد.
- تابع در نقاطی که پیوستهاند ولی مشتق در آنها به سمت عدد مشخصی میل نمیکند نیز مشتقناپذیر است. از دید هندسی، در این نقاط نمیتوان مماس مشخصی بر منحنی رسم کرد.
دامنهٔ تابع مشتق
منظور از دامنهٔ تابع مشتق مجموعهٔ نقاطی است که تابع در آنها مشتقپذیر است. به طور کلی برای تابع  داریم:
داریم:
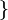 مجموعه نقاطی که
مجموعه نقاطی که 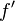 در آن تعریف نشده است
در آن تعریف نشده است 
مشتق تابع نسبت به تابع
هرگاه بخواهیم مشتق یک تابع مانند  را نسبت به تابع دیگری مانند
را نسبت به تابع دیگری مانند 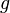 بدست آوریم، کافی است مشتق این توابع را نسبت به متغیرشان محاسبه نموده و سپس بر هم تقسیم کنیم.
بدست آوریم، کافی است مشتق این توابع را نسبت به متغیرشان محاسبه نموده و سپس بر هم تقسیم کنیم.
مشتق توابع پارامتری
توابع که به فرم 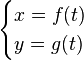 هستند را توابع پارامتری مینامند. در این حالت، مشتق
هستند را توابع پارامتری مینامند. در این حالت، مشتق 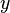 نسبت به
نسبت به  از رابطهٔ زیر قابل محاسبه است:
از رابطهٔ زیر قابل محاسبه است:
قضیهٔ لاگرانژ
قضیهٔ لاگرانژ یا مقدار میانگین مشتق بیان میکند که هرگاه تابع  روی
روی ![[a , b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) پیوسته و روی بازهٔ
پیوسته و روی بازهٔ 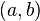 مشتقپذیر باشد، آنگاه حداقل یک نقطهٔ
مشتقپذیر باشد، آنگاه حداقل یک نقطهٔ  در بازهٔ
در بازهٔ 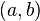 وجود دارد که در آن:
وجود دارد که در آن:
- تعبیر هندسی: قضیه بیان میکند که در بازهٔ
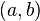 حداقل یک نقطه وجود دارد که مماس بر منحنی در آن نقطه به موازات خط واصل نقاط دو سر منحنی است.
حداقل یک نقطه وجود دارد که مماس بر منحنی در آن نقطه به موازات خط واصل نقاط دو سر منحنی است. - تعبیر فیزیکی: اگر نمودار را مکان-زمان در نظر بگیریم و بازهٔ
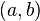 بازهٔ زمانی باشد، قضیهٔ فوق میگوید، حداقل یک لحظه در بازهٔ
بازهٔ زمانی باشد، قضیهٔ فوق میگوید، حداقل یک لحظه در بازهٔ 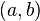 وجود دارد که سرعت لحظهای با سرعت متوسط برابر میشود.
وجود دارد که سرعت لحظهای با سرعت متوسط برابر میشود.
قضیهٔ کوشی
قضیهٔ کوشی که صورت تعمیم یافتهٔ قضیهٔ لاگرانژ است، بیان میکند که هرگاه توابع  و
و 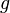 روی بازهٔ
روی بازهٔ ![[a , b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) پیوسته و روی بازهٔ
پیوسته و روی بازهٔ 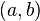 مشتقپذیر باشند، آنگاه حداقل یک نقطهٔ
مشتقپذیر باشند، آنگاه حداقل یک نقطهٔ  در بازهٔ
در بازهٔ 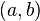 وجود دارد که در آن:
وجود دارد که در آن:
کاربرد مشتق
خط مماس و قائم
مشتق به ازای مختصات نقطهٔ تماس برابر است با ضریب زاویهٔ خط مماس. پس برای تعیین شیب خط مماس یا قائم بر منحنی و تعیین معادلهٔ آنها میتوان از مشتق استفاده کرد.
معادلهٔ خط مماس در نقطهٔ  واقع بر منحنی:
واقع بر منحنی:
معادلهٔ خط قائم در نقطهٔ  واقع بر منحنی:
واقع بر منحنی:
معادلهٔ خط مماس بر منحنی از نقطهای خارج از منحنی: اگر بخواهیم از نقطهٔ  مماسی بر منحنی رسم کنیم، نقطهٔ تماس را
مماسی بر منحنی رسم کنیم، نقطهٔ تماس را  در نظر میگیریم، چون نقطهٔ
در نظر میگیریم، چون نقطهٔ  روی منحنی قرار گرفته از منحنی مشتق میگیریم و مختصات
روی منحنی قرار گرفته از منحنی مشتق میگیریم و مختصات  را قرار میدهیم تا شیب معادله بدست آید.
را قرار میدهیم تا شیب معادله بدست آید.
در نهایت چون نقطهٔ  روی خط مماس قرار دارد، در معادلهٔ فوق قرار داده تا یک معادلهٔ یک مجهولی بر حسب
روی خط مماس قرار دارد، در معادلهٔ فوق قرار داده تا یک معادلهٔ یک مجهولی بر حسب  بدست آید.
بدست آید.
آهنگ تغییر
نسبت تغییرات دو کمیت را آهنگ تغییر یکی نسبت به دیگری میگویند.
آهنگ تغییر متوسط
آهنگ متوسط تغییرات  در فاصلهٔ
در فاصلهٔ ![[a , b] \!](http://upload.wikimedia.org/math/5/2/d/52d4fce11e59f0395730bb90f9b239cc.png) عبارت است از:
عبارت است از:
آهنگ متوسط تغییرات  نسبت به متغیر
نسبت به متغیر  عبارت است از:
عبارت است از:
آهنگ تغییر لحظهای
اگر  تغییرات
تغییرات  نسبت به تغییرات
نسبت به تغییرات  را آهنگ آنی (لحظهای) تغییر
را آهنگ آنی (لحظهای) تغییر  نسبت به
نسبت به  گویند.
گویند.
آزمونهای مشتق
آزمون مشتق اول
با فرض اینکه  نقطهٔ بحرانی تابع
نقطهٔ بحرانی تابع  است و
است و  و
و  روی
روی 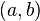 پیوسته و به جز احتمالاً در
پیوسته و به جز احتمالاً در  مشتقپذیر باشد:
مشتقپذیر باشد:
- اگر
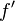 روی
روی  مثبت و روی
مثبت و روی  منفی باشد، آنگاه
منفی باشد، آنگاه  در
در  ماکزیمم نسبی دارد.
ماکزیمم نسبی دارد. - اگر
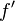 روی
روی  منفی و روی
منفی و روی  مثبت باشد، آنگاه
مثبت باشد، آنگاه  در
در  مینیمم نسبی دارد.
مینیمم نسبی دارد. - اگر
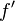 روی
روی  و
و  همعلامت باشد، آنگاه
همعلامت باشد، آنگاه  در
در  اکسترمم ندارد.
اکسترمم ندارد.
آزمون مشتق دوم
فرض کنید  نقطهٔ بحرانی تابع
نقطهٔ بحرانی تابع  و
و  موجود باشد:
موجود باشد:
- اگر
 باشد آنگاه
باشد آنگاه  در
در  دارای
دارای  نسبی است.
نسبی است. - اگر
 باشد آنگاه
باشد آنگاه  در
در  دارای
دارای  نسبی است.
نسبی است. - اگر
 باشد آزمون بینتیجه است.
باشد آزمون بینتیجه است.
جهت تقعر و نقطهٔ عطف
اگر نمودار تابعی به صورت  باشد، تقعر آن به سمت بالاست. در این حالت منحنی بالای هر خطی که بر آن مماس شود، قرار میگیرد. به عبارت دیگر اگر
باشد، تقعر آن به سمت بالاست. در این حالت منحنی بالای هر خطی که بر آن مماس شود، قرار میگیرد. به عبارت دیگر اگر 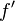 صعودی اکید باشد و یا
صعودی اکید باشد و یا  روی بازهٔ
روی بازهٔ  موجود و همواره مثبت باشد، آنگاه جهت تقعر نمودار
موجود و همواره مثبت باشد، آنگاه جهت تقعر نمودار  روی این بازه رو به بالاست.
روی این بازه رو به بالاست.
اگر نمودار تابعی به صورت  باشد، تقعر آن به سمت پایین است. در این حالت منحنی پایین هر خطی که بر آن مماس شود، قرار میگیرد. به عبارت دیگر اگر
باشد، تقعر آن به سمت پایین است. در این حالت منحنی پایین هر خطی که بر آن مماس شود، قرار میگیرد. به عبارت دیگر اگر 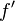 نزولی اکید باشد و یا
نزولی اکید باشد و یا  روی بازهٔ
روی بازهٔ  موجود و همواره منفی باشد، آنگاه جهت تقعر نمودار
موجود و همواره منفی باشد، آنگاه جهت تقعر نمودار  روی این بازه رو به پایین است.
روی این بازه رو به پایین است.
نقطهٔ عطف
اگر جهت تقعر نمودار  در نقطهٔ
در نقطهٔ  تغییر کند و مماس نیز داشته باشد، آنگاه
تغییر کند و مماس نیز داشته باشد، آنگاه  را نقطهٔ عطف گویند. در بررسی نقطهٔ عطف تابع، سه شرط زیر باید برقرار باشد:
را نقطهٔ عطف گویند. در بررسی نقطهٔ عطف تابع، سه شرط زیر باید برقرار باشد:
 در
در  پیوسته باشد.
پیوسته باشد. در
در  فقط یک مماس داشته باشد. (مایل، افقی یا قائم)
فقط یک مماس داشته باشد. (مایل، افقی یا قائم)- جهت تقعر
 در
در  تغییر کند.
تغییر کند.
پس برای یافتن نقاط عطف نمودار تابع کافی است، نقاطی که  در آنها وجود ندارد یا برابر صفر است را تعیین و علامت
در آنها وجود ندارد یا برابر صفر است را تعیین و علامت  را قبل و بعد از این نقاط و نیز وجود خط مماس را در این نقاط بررسی کنیم.
را قبل و بعد از این نقاط و نیز وجود خط مماس را در این نقاط بررسی کنیم.
بهینهسازی
بسیاری از مسائلی که در علوم تجربی و ریاضیات مطرح میشوند، در جستجوی یافتن مقادیر ماکزیمم و مینیممی هستند که یک تابع مشتقپذیر میتواند در دامنهٔ خاص اختیار کند و مشتق ابزار مناسبی برای یافتن این مقادیر است.
برای حل مسائل بهینهسازی لازم است ابتدا کمیتهایی مانند حجم، مساحت، فاصله و... که بیشترین یا کمترین مقدار آن مورد نیاز است، به صورت تابعی از متغیرهای دیگر نوشته شود و چنانچه معادلهٔ حاصل بیش از یک متغیر داشت با استفاده از فرضیات مسأله و ارتباط متغیرها با هم، معادله را به معادلهای با یک متغیر مستقل تبدیل کرد و در انتها به کمک مشتق، نقاط بحرانی را یافت، تا بتوان ماکزیمم و مینیمم مطلق تابع را مشخص کرد.
قواعد مشتقگیری
در روابط زیر 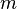 ،
، و
و  اعداد ثابت،
اعداد ثابت، 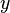 ،
، ،
،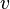 ،
، ،
،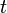 متغیر و
متغیر و  عدد نپر است.
عدد نپر است.
توابع جبری
|
|




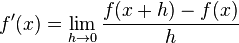
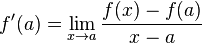




















 (قاعدهٔ توان)
(قاعدهٔ توان) (قاعدهٔ حاصلضرب)
(قاعدهٔ حاصلضرب)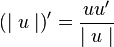
![\left ( \sqrt[m]{u} \; \right )' = \frac{u'}{m \sqrt[m]{u^{m-1}}} \!](http://upload.wikimedia.org/math/5/1/b/51b673363d7fd9dc11359210b3f569b8.png)
 (قاعدهٔ ضریب ثابت)
(قاعدهٔ ضریب ثابت) (قاعدهٔ مجموع)
(قاعدهٔ مجموع) (قاعدهٔ خارجقسمت)
(قاعدهٔ خارجقسمت)
![\left ( \sqrt[m]{u^p} \; \right )' = \frac{pu'}{m \sqrt[m]{u^{m-p}}} \!](http://upload.wikimedia.org/math/f/6/2/f62c18f452ce8cf29f649f5dbb342b89.png)

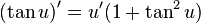
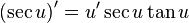


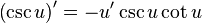











سلامت باشی. اگه یه نفر باشه که برای این مطالب مهم وقت بذاره اون خودتی
واقعن خداقوت!